优化快速排序_优化快速排序的方法

优化快速排序_优化快速排序的方法

       大家好，今天我来为大家详细地介绍一下关于优化快速排序的问题。以下是我对这个问题的总结和归纳，希望能对大家有所帮助。

1.快速排序的基本思想

2.c++快速排序详解

3.八大经典排序算法原理及实现

4.数据结构中快速排序算法的不足以及改进？

5.排序（二）希尔排序、归并排序、快速排序

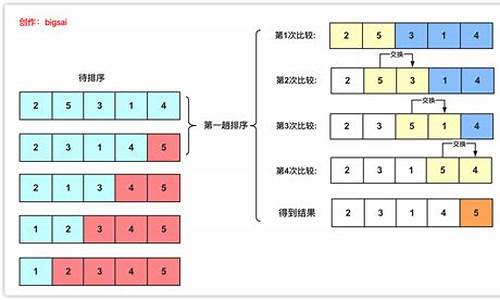
快速排序的基本思想

       快速排序的基本思想：

       快速排序基本思想是采用分治法。具体来说，它将一个大的数组分成两个子数组，将子数组分别进行排序，然后再将排好序的子数组进行合并，得到最终的排序结果。

       快速排序的核心在于分区操作，即如何将一个大的数组分成两个子数组，使得其中一个子数组的所有元素都小于另一个子数组的所有元素。这个分区操作可以通过一趟扫描完成。在扫描过程中，从数组的第一个元素开始，比较当前元素和其后面的元素的大小。

       如果当前元素比后面的元素小，则交换它们的位置。这样一趟扫描下来，最大的元素就会被移到数组的最后一个位置。接着再分别对剩下的两个子数组进行同样的扫描操作，直到整个数组被排好序为止。

       快速排序的时间复杂度为O（nlogn），其中n是数组的大小。它的优点在于速度快，时间复杂度比其他线性排序算法要低。同时，由于它是一种原地排序算法，不需要额外的存储空间，因此在空间复杂度上也较为优秀。

       然而，快速排序在最坏情况下的时间复杂度为O（n^2），这种情况通常发生在输入的数组已经有序或者接近有序的情况下。为了避免这种情况，可以通过一些优化手段来提高算法的效率，例如随机化分区函数或者使用三数取中法来选择分区点。

快速排序优势：

       1、高效快速：快速排序的时间复杂度通常为O（nlogn），在大多数情况下，它的速度比其他线性排序算法更快。快速排序的优秀性能使得它在大量数据排序时非常高效。

       2、原地排序：快速排序是原地排序算法，不需要额外的存储空间。这意味着它可以在有限的内存空间中处理大数据集，特别适用于内存受限的环境。

       3、简单易理解：快速排序的算法实现简单，易于理解和实现。无论是初学者还是资深开发者，都可以轻松地理解和实现快速排序。

       4、适应性强：快速排序在各种场景下表现出色，无论是数值还是字符串数组，都可以使用快速排序进行排序。此外，快速排序还适用于各种不同的数据类型，具有广泛的适用性。

       5、稳定的排序：快速排序是一种稳定的排序算法，这意味着相等的元素在排序后保持其原始顺序。这对于需要保持特定顺序的场景非常有用。

       6、可扩展性强：快速排序具有良好的可扩展性，可以轻松地并行化和分布式处理。这使得在处理大规模数据集时，快速排序可以充分利用多核CPU和分布式计算资源，提高排序效率。

       7、随机化快速排序：为了避免最坏情况的出现，可以引入随机化快速排序。通过随机选择枢轴元素，可以使得算法在各种输入下都保持较好的性能。

c++快速排序详解

       现如今，快排技术没有更新的，就炸了，目前seo这个词，上排名，小明seo，孔宇科技等，皆为在百度首页，因为他们有更新过百度快排技术，百度算法怎么改，他们就去迎合。进而掉了排名之后，鸡儿雄起的贼快。

       有人说快排是一种黑猫seo作弊的行为，然而真的这样嘛？其实确实是有，好的快排系统上词快，死得更快。但是有的快排系统还是比较稳定的，其实，他们就很迎合百度的算法了，以及各大搜索引擎的算法。一旦快排他们爹：百度，生气了要大改，他们儿子快排都得跪下来，有时候快排他们爹，就打几下喷嚏，儿子快排，排名瞬间消失几天，他们都敢怒不敢言。

       总体来说，你想正常做网站优化，是最好的，千万别没事有事玩什么快排排名，虽然说，这段时间，你排名上得快，说不定你下一秒就0排名。

       不过这也不一定啦，看你们怎么想快排了，有些人利用快排技术，也赚到了很多钱，此时此刻，你应该每天烧点香，每天默念百度爹真好。

八大经典排序算法原理及实现

       　基本思想： 通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分所有数据要小，然后再按此方法对这两部分数据分别进行快速排序。整个排序过程可以递归进行，以此达到整个数据变成有序序列。

       　将数列变成上述形式，这一步很关键，做好这一步，才能对主元左右的部分进行递归调用。以下是实现这一部分的代码：

       　int partition_sort(int arr[],int l,int r)//l是数组最左边，r为最右边

       　{

       　int j=l;//设计标记

       　int t=arr[l];//设置主元

       　for(int i=l+1;i<=r;i++)

       　{

       　if(arr[i]<t){

       　swap(arr[j+1],arr[i]);

       　j++;

       　}

       　}

       　swap(arr[l],arr[j]);

       　return j;

       　}

       　上述代码中，我把最左边的元素当作主元，这样的代码对大多数排序都很高效，但是不排除个别情况（当数组近乎有序或者当数组内有大量重复元素），这时，我们的排序算法相比于归并排序显得并不是那么高效，这和我们的`排序算法原理密不可分，细细分析，当数组近乎有序时，我们的快速排序竟然退化到了O（n^2)级别，这显然是非常不高效的。

       　要想实现上述不足的优化，我们可以将主元随机选择，或者采用其他方式的快速排序（双路快速排序，三路快速排序），本篇内容仅作为学习快排的基本思想和基本实现，不深入涉及，有兴趣的读者可查阅资料了解。

下面是全部的实现代码：

       　#include <iostream>

       　#include <math.h>

       　using namespace std;

       　//实现函数，用于partition的递归

       　int partition_sort(int arr[],int l,int r)//l是数组最左边，r为最右边

       　{

       　int j=l;//设计标记

       　int t=arr[l];//设置主元

       　for(int i=l+1;i<=r;i++)

       　{

       　if(arr[i]<t){

       　swap(arr[j+1],arr[i]);

       　j++;

       　}

       　}

       　swap(arr[l],arr[j]);

       　return j;

       　}

       　//实现递归的调用函数

       　void partition(int arr[],int l,int r)

       　{

       　if(l>=r)return ;

       　int p=partition_sort(arr,l,r);

       　partition(arr,l,p-1);

       　partition(arr,p+1,r);

       　}

       　int main()

       　{

       　int a[5];

       　for(int i=0;i<5;i++)

       　{

       　cin>>a[i];

       　}

       　partition(a,0,4);

       　for(int i=0;i<5;i++)

       　{

       　cout<<a[i]<<" ";

       　}

       　return 0;

       　}

数据结构中快速排序算法的不足以及改进？

        该系列文章主要是记录下自己暑假这段时间的学习笔记，暑期也在实习，抽空学了很多，每个方面的知识我都会另起一篇博客去记录，每篇头部主要是另起博客的链接。

        冒泡排序算法应该是大家第一个接触的算法，其原理都应该懂，但我还是想以自己的语言来叙述下其步奏：

        按照计算时间复杂度的规则，去掉常数、去掉最高项系数，其复杂度为O(N^2)

        冒泡排序及其复杂度分析

        空间复杂度就是在交换元素时那个临时变量所占的内存

        给定一个整数序列{6,1,2,3,4},每完成一次外层循环的结果为：

        我们发现第一次外层循环之后就排序成功了，但是还是会继续循环下去，造成了不必要的时间复杂度，怎么优化？

        冒泡排序都是相邻元素的比较，当相邻元素相等时并不会交换，因此冒泡排序算法是稳定性算法

        插入排序是对冒泡排序的一种改进

        插入排序的思想是数组是部分有序的，再将无序的部分插入有序的部分中去,如图：

        （来自 这里 ）

        空间复杂度就是在交换元素时那个临时变量所占的内存

        插入排序的优化，有两种方案：

        文章后面会给出这两种排序算法

        由于插入排序也是相邻元素的比较，遇到相等的相邻元素时不会发生交换，也不会造成相等元素之间的相对位置发生变化

        其原理是从未排序的元素中选出最小值(最大值)放在已排序元素的后面

        空间复杂度就是在交换元素时那个临时变量所占的内存

        选择排序是不稳定的，比如 3 6 3 2 4，第一次外层循环中就会交换第一个元素3和第四个元素2，那么就会导致原序列的两个3的相对位置发生变化

        希尔排序算是改良版的插入排序算法，所以也称为希尔插入排序算法

        其原理是将序列分割成若干子序列（由相隔某个增量 的元素组成的），分别进行直接插入排序；接着依次缩小增量继续进行排序，待整个序列基本有序时，再对全体元素进行插入排序，我们知道当序列基本有序时使用直接插入排序的效率很高。

        上述描述只是其原理，真正的实现可以按下述步奏来：

        希尔排序的效率取决于增量值gap 的选取，这涉及到数学上尚未解决的难题，但是某些序列中复杂度可以为O(N 1.3)，当然最好肯定是O(N)，最坏是O(N 2)

        空间复杂度就是在交换元素时那个临时变量所占的内存

        希尔排序并不只是相邻元素的比较，有许多跳跃式的比较，难免会出现相同元素之间的相对位置发生变化，所以希尔排序是不稳定的

        理解堆排序，就必须得先知道什么是堆？

        二叉树的特点：

        当父节点的值总是大于子结点时为最大堆 ；反之为最小堆 ，下图就为一个二叉堆

        一般用数组来表示堆，下标为 i 的结点的父结点下标为(i-1)/2；其左右子结点分别为 (2 i + 1)、(2 i + 2)

        怎么将给定的数组序列按照堆的性质，调整为堆？

        这里以建立最小堆为示例，

        很明显对于其叶子结点来说，已经是一个合法的子堆，所以做堆调整时，子节点没有必要进行，这里只需从结点为A[4] = 50的结点开始做堆调整，即从（n/2 - 1）位置处向上开始做堆调整：

        由于每次重新恢复堆的时间复杂度为O(logN)，共N - 1次重新恢复堆操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)，二次操作时间相加还是O(N logN)。故堆排序的时间复杂度为O(N * logN)。

        空间复杂度就是在交换元素时那个临时变量所占的内存

        由于堆排序也是跨越式的交换数据，会导致相同元素之间的相对位置发生变化，则算法不稳定。比如 5 5 5 ,堆化数组后将堆顶元素5与堆尾元素5交换，使得第一个5和第三个5的相对位置发生变化

        归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

        快速排序在应该是大家经常看到、听到的算法，但是真正默写出来是有难度的。希望大家看了下面挖坑填数 方法后，能快速写出、快速排序。

        其原理就这么几句话，但是现实起来并不是这么简单，我们采取流行的一种方式挖坑填数分治法

        对于序列： 72 6 57 88 60 42 83 73 48 85

        数组变为：48 6 57 88 60 42 83 73 88 85

        再重复上面的步骤，先从后向前找，再从前向后找：

        数组变为：48 6 57 42 60 72 83 73 88 85

        可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了

        空间复杂度，主要是递归造成的栈空间的使用:

        快速排序的优化主要在于基准数的选取

        快速排序也是跨越式比较及交换数据，易导致相同元素之间的相对位置发生变化，所以快速排序不稳定

        前面也说了二分查找排序是改进的插入排序，不同之处在于，在有序区间查找新元素插入位置时，为了减少比较次数提高效率，采用二分查找算法进行插入位置的确定

        具体步骤，设数组为a[0…n]：

        二分查找插入位置，因为不是查找相等值，而是基于比较查插入合适的位置，所以必须查到最后一个元素才知道插入位置。

        二分查找最坏时间复杂度：当2^X>=n时，查询结束，所以查询的次数就为x，而x等于log2n（以2为底，n的对数）。即O(log2n)

        所以，二分查找排序比较次数为：x=log2n

        二分查找插入排序耗时的操作有：比较 + 后移赋值。时间复杂度如下：

        二分查找排序在交换数据时时进行移动，当遇到有相等值插入时也只会插入其后面，不会影响其相等元素之间的相对位置，所以是稳定的

        白话经典算法排序

        冒泡排序选择排序

        快速排序复杂度分析

        优化的插入排序

排序（二）希尔排序、归并排序、快速排序

       一般快速排序算法都是以最左元素作为划分的基准值，这样当数据元素本身已经完全有序（不管正序或者逆序）时，每一趟划分只能将一个元素分割出来，其效率很低：时间复杂度O(n^2)，空间复杂度为O(n)

       所以改进方法就是找寻合适的基准值，保证不至于在关键字有序或者接近有序时发生这个情况，一般可以使用三者取中（就是待划分序列的头元素、尾元素、中间元素三者的中间值）、或者随机选择等方法，这样即使关键字完全有序，也可以保证时间复杂度O(nlogn)，空间复杂度O(logn)

       希尔排序是对插入排序的优化。希尔排序的思想：先使用数组中任间隔为h的元素有序，然后对全局进行排序。

        h该怎么取值呢？如果数组长度比较小，则可设置 h=3，h=1。若数组长度比较大，可以取 h=4，但最终还是得对全局进行排序：h=1。但如果数组很长呢？则可以设置 h=10，h=4，h=1。那如果再来一个数组更加大的呢？则可以对h=22，h=10，h=4，h=1（全局排序）进行排序。所以说h的取值是一个递增序列。

        我们要对一个大规模的数组进行间隔排序，再全局排序（h=1），最终得到有序的数组。

        我们用其中最常用的这个。对应的时间复杂度是： 。（不推倒了，记一下）

        data数组有16个元素，下面是对data中的元素进行排序：

        h=4时，

        开始：i从i=4，即i从数组第5个元素开始；j=i 比较j和j-4，如果是升序的，就不做任何交换了。

        下一个元素：i=5，j从i开始，比较j和j-4，看是否需要交换。

        ...

        i=8，j从i开始，将j，j-4，j-8，(间隔为4的元素)的进行排序。排序过程：先将j和j-4比较，看是否需交换；再将j-4和j-8进行比较，看是否需要交换。

        ....

        h=1时，

        开始：i从i=1，j从i开始，比较j和j-1，看是否需要交换。

        i=2，j从i开始，将j，j-1，j-2，(间隔为1的元素)的进行排序。排序过程：先将j和j-1比较，看是否需交换；再将j-1和j-2进行比较，看是否需要交换。

        ....

        i=13，j从i开始，将j，j-1，j-2，... (间隔为1的元素)的进行排序。排序过程：先将j和j-1比较，看是否需交换；再将j-1和j-2进行比较，看是否需要交换...

        为了降低空间复杂度，也可以这样写：

        另一种写法，开始时，将data中元素拷贝到tmp中，再对data中的元素进行操作。

        归并排序总时间=子序列排好序时间+合并时间

       自底向上的归并排序不是重点，把之前的那个自顶向下的归并排序弄精通了就行啦。

        找到一个pivot分区点，将小于分区点的排到pivot前面，将大于分区点的排到pivot后面。

        那么，如何将左边的子数组排序？还是在子数组里选择一个分区点，将小于分区点的放到前面，大于分区点的放到后面。

        递推公式：sort(data, lo, hi)

        当分区点选择不合理，快排的时间复杂度退化为 。比如，在升序序列中，将最后一个元素设为pivot。

        当数组中有大量重复元素，上述方法会增加不必要的排序。

       好了，今天关于“优化快速排序”的话题就讲到这里了。希望大家能够通过我的讲解对“优化快速排序”有更全面、深入的了解，并且能够在今后的学习中更好地运用所学知识。